Por Domingos Sávio de Lima Soares*
De BH
1. Introdução
Albert Einstein (1879-1955) apresentou a Teoria da Relatividade Restrita (TRR) em 1905, e pouco tempo depois o matemático alemão Hermann Minkowski (1864–1909), seu antigo professor em Zurique, mostrou que ela, originalmente proposta em forma algébrica, poderia ser entendida geometricamente como uma teoria do espaço-tempo tetradimensional (três coordenadas espaciais mais uma temporal).
A seção espacial deste espaço-tempo é o trivial espaço euclidiano, cuja característica mais típica é a de ser geometricamente plano, ou seja, a de obedecer aos postulados e corolários da geometria euclidiana (por exemplo, a soma dos ângulos internos de um triângulo é igual a 180 graus, o perímetro de um círculo dividido pelo seu diâmetro é igual ao número irracional π, por um ponto fora de uma reta passa uma e somente uma reta paralela, etc).
O espaço tetradimensional da TRR é denominado, por razões óbvias, espaço-tempo de Minkowski. Na verdade, ele nada mais é do que uma extensão do espaço euclidiano tridimensional para quatro dimensões e é também, portanto, geometricamente plano. A propósito, o espaço euclidiano pode ser estendido para qualquer número de dimensões n.
A métrica de um espaço n-dimensional qualquer é a expressão matemática que permite o cálculo de distâncias neste espaço. Assim a métrica do espaço euclidiano tridimensional, em coordenadas cartesianas, é dada pela expressão da distância infinitesimal ds entre os pontos (x,y,z) e (x+dx,y+dy,z+dz):
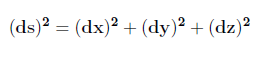 | . (1) |
2. Teoria da Relatividade RestritaA TRR é uma teoria geométrica de um espaço tetradimensional plano, o espaço-tempo de Minkowski. A sua métrica, caracterizando-o como um espaço plano, é dada pela distância infinitesimal entre dois eventos localizados em (x,y,z,t) e (x+dx,y+dy,z+dz,t+dt):
onde c é a velocidade da luz no vácuo e o sinal negativo no termo temporal é adotado por convenção e conveniência. No caso de um intervalo nulo ds = 0, teremos c=±dl/dt, com (dl)² = (dx)² + (dy)² + (dz)², ou seja, somente a luz poderia viajar entre os dois eventos. Por extensão, definimos a geodésica nula ougeodésica tipo luz como o caminho entre dois eventos quaisquer, para os quais Δs=0. Para o espaço-tempo de Minkowski, a geodésica nula é um segmento de linha reta.
A seção espacial do espaço-tempo de Minkowski — e de qualquer outro espaço-tempo — é obtida “congelando-se” o tempo, i.e., fazendo-se t = constante, ou dt = 0, na Eq. 2. Obtemos, neste caso, o espaço plano euclidiano tridimensional, cuja métrica é dada pela Eq. 1.
Então, podemos dizer que na TRR o espaço-tempo e o espaço são planos. Isto não será verdadeiro para as soluções da TRG discutidas a seguir. Para elas, o espaço-tempo será sempre curvo e o espaço será, geralmente, também curvo. Veremos apenas um caso em que a seção espacial de uma solução da TRG será plana.
A seção espacial do espaço-tempo de Minkowski — e de qualquer outro espaço-tempo — é obtida “congelando-se” o tempo, i.e., fazendo-se t = constante, ou dt = 0, na Eq. 2. Obtemos, neste caso, o espaço plano euclidiano tridimensional, cuja métrica é dada pela Eq. 1.
Então, podemos dizer que na TRR o espaço-tempo e o espaço são planos. Isto não será verdadeiro para as soluções da TRG discutidas a seguir. Para elas, o espaço-tempo será sempre curvo e o espaço será, geralmente, também curvo. Veremos apenas um caso em que a seção espacial de uma solução da TRG será plana.
3. Teoria da Relatividade Geral
A Teoria da Relatividade Geral (TRG) é uma teoria geométrica de um espaço tetradimensional curvo, cuja seção espacial pode ser plana ou curva, como veremos a seguir em dois exemplos. O espaço-tempo curvo da TRG implica em que um corpo de prova colocado em repouso em qualquer ponto do espaço sairá do repouso, ou seja, ele “rola” pelo espaço-tempo curvo afora. A situação é análoga ao que ocorre na mecânica newtoniana, quando um corpo de prova é colocado em repouso numa região do espaço onde existe um campo de força. Alternativamente, um corpo de prova colocado em repouso num espaço-tempo plano permanece em repouso, um comportamento análogo ao ditado pela Primeira Lei da mecância newtoniana.
3.1. A solução de Schwarzschild
Logo após a apresentação final da TRG em 1916, o astrônomo alemão Karl Schwarzschild (1873-1916) resolveu as equações de campo de Einstein para um caso bastante particular, simples e de grande alcance quanto às suas possibilidades de aplicações experimental e observacional. Trata-se da determinação da métrica do espaço-tempo no exterior de uma distribuição de massa M, estática e esfericamente simétrica. A solução de Schwarzschild aplica-se, por exemplo, para o movimento planetário em torno do Sol, e representa um aperfeiçoamento da lei de gravitação universal de Newton quando aplicada no mesmo contexto.
Devido à simetria do problema — um corpo central esférico — a métrica de Schwarzschild é convenientemente expressa em coordenadas esféricas. O intervalo espácio-temporal ds será dado por:
onde r, θ e ϕ são as coordenadas esféricas usuais. Note que a geodésica nula é curva e não um segmento de reta como na métrica de Minkowski. Para se certificar disto, compare a parte espacial da métrica da Eq. 3 com a parte espacial da métrica de Minkowski em coordenadas esféricas, (ds)² = −(cdt)² + (dr)² + (rdθ)² + (rsenθdϕ)², e veja que elas são diferentes.
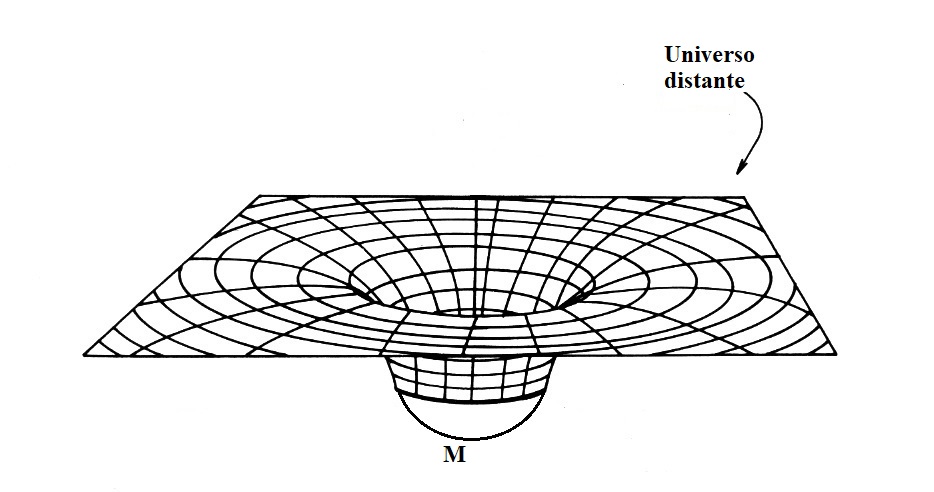
Para a visualização da seção espacial do espaço-tempo de Schwarzschild faremos como Edwin Taylor e John A. Wheeler em seu livro Exploring black holes – Introduction to General Relativity de 2000. No capítulo 2, seção 10, pág. 2-24, intitulada Picturing the space part of Schwarzschild geometry, os autores restringem-se a duas dimensões espaciais (r e θ, fixando ϕ, dϕ = 0), para uma visualização 2D imersa no espaço 3D. Desta forma, o resultado é um parabolóide de revolução em torno da massa central M (veja Fig. 1).
3.2. As soluções de Friedmann
Devido à simetria do problema — um corpo central esférico — a métrica de Schwarzschild é convenientemente expressa em coordenadas esféricas. O intervalo espácio-temporal ds será dado por:
Para a visualização da seção espacial do espaço-tempo de Schwarzschild faremos como Edwin Taylor e John A. Wheeler em seu livro Exploring black holes – Introduction to General Relativity de 2000. No capítulo 2, seção 10, pág. 2-24, intitulada Picturing the space part of Schwarzschild geometry, os autores restringem-se a duas dimensões espaciais (r e θ, fixando ϕ, dϕ = 0), para uma visualização 2D imersa no espaço 3D. Desta forma, o resultado é um parabolóide de revolução em torno da massa central M (veja Fig. 1).
 |
Representação bidimensional da seção espacial do espaço-tempo de Schwarzschild. |
Uma característica interessante da métrica de Schwarzschild é que, sendo a geodésica nula curva, podemos ter a ocorrência de dois fenômenos inéditos, em relação à física clássica: a deflexão da luz ao passar próxima a uma massa M e a lente gravitacional — também uma consequência da deflexão da luz. O fenômeno das lentes gravitacionais origina efeitos ainda mais esdrúxulos tais como miragens, amplificação da intensidade luminosa, etc.
Concluindo, o espaço-tempo de Schwarzschild e a sua seção espacial são ambos curvos.
Concluindo, o espaço-tempo de Schwarzschild e a sua seção espacial são ambos curvos.
3.2. As soluções de Friedmann
O atual Modelo Padrão da Cosmologia (MPC) é a modificação de um dos modelos relativístas históricos, quais sejam, aqueles desenvolvidos pelo cosmólogo russo Alexander Friedmann (1888-1925), logo após a proposta da TRG por Einstein. Friedmann publicou os seus estudos no início da década de 1920. Os seus modelos eram soluções particulares das equações de campo da TRG aplicadas ao universo sob uma hipótese simplificadora, que ficou conhecida posteriormente como “Princípio Cosmológico” (para uma visão geral do procedimento de Friedmann veja Os primeiros passos na cosmologia relativista). Posteriormente, o matemático e físico norte-americano Howard Robertson (1903–1961) e o matemático inglês Arthur Walker (1909–2001) mostraram, independentemente, em meados da década de 1930, que as soluções de Friedmann eram caracterizadas pela métrica espácio-temporal mostrada na Eq. 4. Devido às simetrias introduzidas pelo Princípio Cosmológico, esta métrica, que ficou conhecida como métrica de Friedmann-Robertson-Walker, é, também, mais apropriadamente expressa em coordenadas esféricas:
S(t) é o chamado fator de escala do universo e k é a constante de curvatura da seção espacial. Esta métrica descreve os modelos em expansão típicos do MPC e também admite modelos particulares em contração. Os valores de k podem ser: +1, correspondendo a um universo finito, ilimitado e fechado, −1, a um universo infinito e aberto e 0, a um universo infinito e plano (ou crítico). A geodésica nula é em geral curva, sendo reta apenas para o modelo crítico. Estas três possibilidades estão ilustradas na Fig. 2.
O universo, ou modelo, de Friedmann fechado possui densidade de matéria-energia maior do que a chamada densidade crítica, o universo aberto possui densidade menor do que a densidade crítica, e o universo plano é o modelo cuja densidade é a densidade crítica, e desta forma, a define. Todos estes modelos clássicos de Friedmann estão em expansão desacelerada, sendo que o modelo fechado é cíclico, alternando fases de expansão e contração. O leitor está convidado a ler o artigo Observações sobre as soluções clássicas da equação de Friedmann, onde algumas características dos universos clássicos de Friedmann são discutidas.
Como vimos, então, o espaço-tempo de FRW, dado pela métrica da Eq. 4, é obviamente curvo pois representa uma solução da TRG, e as suas seções espaciais podem ou não ser curvas, dependendo do valor da constante de curvatura k.
| . (4) |
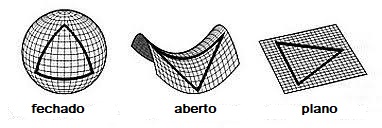 |
Representações bidimensionais das seções espaciais dos espaços-tempos de Friedmann-Robertson-Walker. As somas dos ângulos internos dos triângulos vermelhos são: maior do que 180°, menor do 180° e igual a 180°, para as seções espaciais fechada, aberta e plana, respectivamente. |
Como vimos, então, o espaço-tempo de FRW, dado pela métrica da Eq. 4, é obviamente curvo pois representa uma solução da TRG, e as suas seções espaciais podem ou não ser curvas, dependendo do valor da constante de curvatura k.
4. Considerações finais
Apresento aqui alguns textos que podem complementar e enriquecer a discussão sobre as características do espaço-tempo e do espaço nas teorias relativistas.
A TRG é uma teoria de gravitação e admite inúmeras soluções, cada uma delas referente a uma situação física diferente. Os dois exemplos que mencionamos acima, a saber, a solução de Schwarzschild e a solução de Friedmann são qualitativamente bastante diferentes. A solução de Schwarzschild têm sido comprovada exemplarmente pelas experiências e observações astronômicas e é responsável pelo enorme prestígio de que goza a TRG. Já as soluções cosmológicas de Friedmann ainda não foram comprovadas nem por experiências nem por observações astronômicas, ao contrário do que muitas vezes é apregoado. Uma discussão mais detalhada desta questão qualitativa é apresentada no artigo Uma pedra no caminho da Teoria da Relatividade Geral. Muitas vezes, o sucesso da solução de Schwarzschild é inconscientemente transferido para as cosmologias modificadas de Friedmann, como se elas próprias fossem um sucesso de comprovação observacional. O que de forma alguma é verdadeiro.
Uma curiosidade: a deflexão gravitacional da luz, uma característica original da métrica de Schwarzschild (e da métrica de Friedmann-Robertson-Walker), pode também ser calculada dentro dos preceitos conceituais da mecânica newtoniana. Isto está feito em Newtonian gravitational deflection of light revisited. O resultado para a deflexão da luz originária de uma estrela distante, em incidência rasante à superfície do Sol é, no entanto, duas vezes menor do que o resultado obtido através da solução de Schwarzschild, o qual tem sido brilhantemente comprovado, especialmente pela deflexão de ondas de radiofrequência emitidas por quasares.
A geodésica nula curva no modelo de Friedmann fechado leva à previsão da existência de múltiplas imagens (miragens) de galáxias devido a repetidas “viagens” da luz emitida por elas em trajetórias fechadas, por todo o universo. Este efeito foi bastante explorado em um modelo alternativo ao MPC, formulado pelo cosmólogo francês Jean-Pierre Luminet e colaboradores em 2002 (veja mais detalhes na seção 4 do artigo Espectro de potência da Radiação de Fundo de Micro-ondas).
Uma descrição bem simples da cosmologia dos modelos de Friedmann pode ser vista em O Big Bang, um “Estrondão” no espaço e no tempo. Como foi dito anteriormente, o atual Modelo Padrão da Cosmologia é a modificação de um dos modelos de Friedmann.
A TRG é uma teoria de gravitação e admite inúmeras soluções, cada uma delas referente a uma situação física diferente. Os dois exemplos que mencionamos acima, a saber, a solução de Schwarzschild e a solução de Friedmann são qualitativamente bastante diferentes. A solução de Schwarzschild têm sido comprovada exemplarmente pelas experiências e observações astronômicas e é responsável pelo enorme prestígio de que goza a TRG. Já as soluções cosmológicas de Friedmann ainda não foram comprovadas nem por experiências nem por observações astronômicas, ao contrário do que muitas vezes é apregoado. Uma discussão mais detalhada desta questão qualitativa é apresentada no artigo Uma pedra no caminho da Teoria da Relatividade Geral. Muitas vezes, o sucesso da solução de Schwarzschild é inconscientemente transferido para as cosmologias modificadas de Friedmann, como se elas próprias fossem um sucesso de comprovação observacional. O que de forma alguma é verdadeiro.
Uma curiosidade: a deflexão gravitacional da luz, uma característica original da métrica de Schwarzschild (e da métrica de Friedmann-Robertson-Walker), pode também ser calculada dentro dos preceitos conceituais da mecânica newtoniana. Isto está feito em Newtonian gravitational deflection of light revisited. O resultado para a deflexão da luz originária de uma estrela distante, em incidência rasante à superfície do Sol é, no entanto, duas vezes menor do que o resultado obtido através da solução de Schwarzschild, o qual tem sido brilhantemente comprovado, especialmente pela deflexão de ondas de radiofrequência emitidas por quasares.
A geodésica nula curva no modelo de Friedmann fechado leva à previsão da existência de múltiplas imagens (miragens) de galáxias devido a repetidas “viagens” da luz emitida por elas em trajetórias fechadas, por todo o universo. Este efeito foi bastante explorado em um modelo alternativo ao MPC, formulado pelo cosmólogo francês Jean-Pierre Luminet e colaboradores em 2002 (veja mais detalhes na seção 4 do artigo Espectro de potência da Radiação de Fundo de Micro-ondas).
Uma descrição bem simples da cosmologia dos modelos de Friedmann pode ser vista em O Big Bang, um “Estrondão” no espaço e no tempo. Como foi dito anteriormente, o atual Modelo Padrão da Cosmologia é a modificação de um dos modelos de Friedmann.

Nenhum comentário:
Postar um comentário